Graphing \(y= x^2 -3x -4\)
Step by step guide on how to graph this quadratic equation.
These numbers \( a, b, c\) will be useful for the next few steps.
\(a\) is the number before \(x^2\); \(a=1\)
\(b\) is the number before \(x\). Be sure to include the sign before \(b\); \(b=-3\)
\(c\) is the number that does not have any variable attached to it; \(c=-4\)
\(y= x^2 -3x -4\)
We find the \(x\) coordinate of the vertex by using this formula:
\(x = \frac{-b}{2a}\)
In our case, \( x = \frac{-(-3)}{2\cdot 1} = \frac{3}{2}\)
To find the \(y\) coordinate of the vertex, we substitute this value in the equation and we get:
\(\left(\frac{3}{2}\right)^2 - 3\left(\frac{3}{2}\right) - 4=\frac{-25}{4}\)
So the vertex coordinates are:
\( x = \frac{3}{2}\)
\(y=\frac{-25}{4}\)
Let's add the vertex to the graph.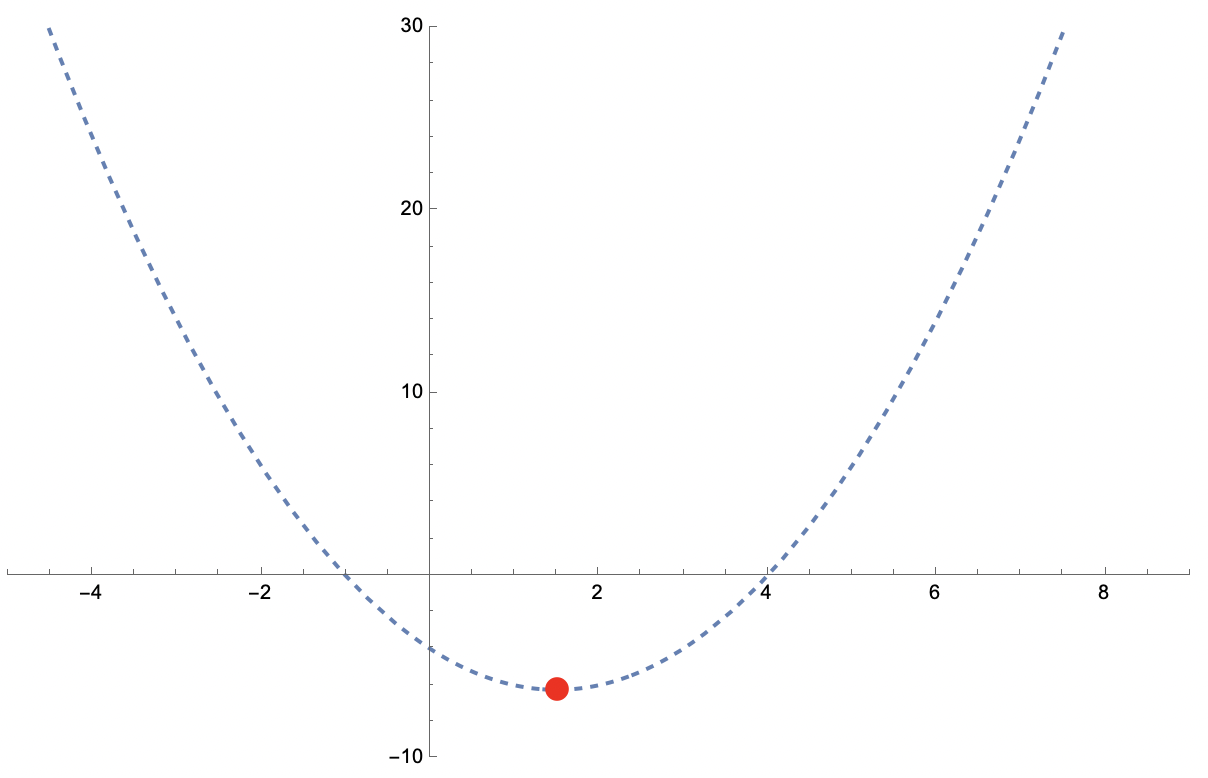
The axis of symmetry helps us build the graph because we can mirror every point on one side of the parabola to the other, without having to make calculations.
The formula of this symmetry line is:
\(x = \frac{-b}{2a}\)
In our case:
\( x = \frac{-(-3)}{2 \cdot 1} = \frac{3}{2}\)
The line \( x = \frac{3}{2}\) will be our axis of symmetry.
Let's draw it.
These are the points where the parabola crosses the x-axis and y-axis.
For the x-intercept, \(y=0\)
\(x^2 - 3x - 4 = 0\)
To solve this equation we can use the discriminant \(\Delta\ = b^2 - 4ac\) and the quadratic formula:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
The 2 roots of this equation are \(-1\) and \(4\), which means that the 2 points where the parabola crosses the x-axis are (\(-1,0\)) and (\(4,0\)). Let's add these points to the graph.
For the y-intercept, \(x=0\). Let's solve for \(y\).
\(0^2 - 3 \cdot 0 - 4 =-4\)
The y-intercept is the point (\(0,-4\)). We add this point to the graph and we "mirror" it using the axis of symmetry.
Let's add all these points to the graph.
Now that we have enough dots, we can connect them to build our parabola. Remember that the parabola is a curve, NOT a straight line.